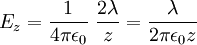Jumat, 23 Juli 2010
20 08 2008
1. Arus
Arus listrik adalah banyaknya muatan listrik yang mengalir tiap satuan waktu. Muatan listrik bisa mengalir melalui kabel atau penghantar listrik lainnya.
I = Q/T
Pada zaman dulu, Arus konvensional didefinisikan sebagai aliran muatan positif, sekalipun kita sekarang tahu bahwa arus listrik itu dihasilkan dari aliran elektron yang bermuatan negatif ke arah yang sebaliknya.
Satuan SI untuk arus listrik adalah ampere (A).
2. Hambatan
Hambatan listrik adalah perbandingan antara tegangan listrik dari suatu komponen elektronik (misalnya resistor) dengan arus listrik yang melewatinya. Hambatan listrik dapat dirumuskan sebagai berikut:
R = V/I
atau
di mana V adalah tegangan dan I adalah arus.
Satuan SI untuk Hambatan adalah Ohm (R).
3. Tegangan
Tegangan listrik (kadang disebut sebagai Voltase) adalah perbedaan potensi listrik antara dua titik dalam rangkaian listrik, dinyatakan dalam satuan volt. Besaran ini mengukur energi potensial sebuah medan listrik untuk menyebabkan aliran listrik dalam sebuah konduktor listrik. Tergantung pada perbedaan potensi listrik satu tegangan listrik dapat dikatakan sebagai ekstra rendah, rendah, tinggi atau ekstra tinggi.
V= I .R
Satuan SI untuk Tegangan adalah volt (V).
4. Hukum OHm
Pada dasarnya sebuah rangkaian listrik terjadi ketika sebuah penghantar mampu dialiri electron bebas secara terus menerus. Aliran yang terus-menerus ini yang disebut dengan arus, dan sering juga disebut dengan aliran, sama halnya dengan air yang mengalir pada sebuah pipa.
Tenaga (the force) yang mendorong electron agar bisa mengalir dalam sebauh rangkaian dinamakan tegangan. Tegangan adalah sebenarnya nilai dari potensial energi antara dua titik. Ketika kita berbicara mengenai jumlah tegangan pada sebuah rangkaian, maka kita akan ditujukan pada berapa besar energi potensial yang ada untuk menggerakkan electron pada titik satu dengan titik yang lainnya. Tanpa kedua titik tersebut istilah dari tegangan tersebut tidak ada artinya.
Elektron bebas cenderung bergerak melewati konduktor dengan beberapa derajat pergesekan, atau bergerak berlawanan. Gerak berlawanan ini yang biasanya disebut dengan hambatan. Besarnya arus didalam rangkaian adalah jumlah dari energi yang ada untuk mendorong electron, dan juga jumlah dari hambatan dalam sebuah rangkaian untuk menghambat lajunya arus. Sama halnya dengan tegangan hambatan ada jumlah relative antara dua titik. Dalam hal ini, banyaknya tegangan dan hambatan sering digunakan untuk menyatakan antara atau melewati titik pada suatu titik.
Untuk menemukan arti dari ketetapan dari persamaan dalam rangkaian ini, kita perlu menentukan sebuah nilai layaknya kita menentukan nilai masa, isi, panjang dan bentuk lain dari persamaan fisika. Standard yang digunakan pada persamaan tersebut adalah arus listrik, tegangan ,dan hambatan.
Symbol yang digunakan adalah standar alphabet yang digunakan pada persamaan aljabar. Standar ini digunakan pada disiplin ilmu fisika dan teknik, dan dikenali secara internasional. Setiap unit ukuran ini dinamakan berdasarkan nama penemu listrik. Amp dari orang perancis Andre M. Ampere, volt dari seorang Italia Alessandro Volta, dan ohm dari orang german Georg Simon ohm.
Simbol matematika dari setiap satuan sebagai berikut “R” untuk resistance (Hambatan), V untuk voltage (tegangan), dan I untuk intensity (arus), standard symbol yang lain dari tegangan adalah E atau Electromotive force. Simbol V dan E dapat dipertukarkan untuk beberapa hal, walaupun beberapa tulisan menggunakan E untuk menandakan sebuah tegangan yang mengalir pada sebuah sumber ( seperti baterai dan generator) dan V bersifat lebih umum.
Salah satu dasar dalam perhitungan elektro, yang sering dibahas mengenai satuan couloumb, dimana ini adalah besarnya energi yang setara dengan electron pada keadaan tidak stabil. Satu couloumb setara dengan 6.250.000.000.000.000.000. electron. Symbolnya ditandai dengan Q dengan satuan couloumb. Ini yang menyebabkan electron mengalir, satu ampere sama dengan 1 couloumb dari electron melewati satu titik pada satu detik. Pada kasus ini, besarnya energi listrik yang bergerak melewati conductor (penghantar).
Sebelum kita mendefinisikan apa itu volt, kita harus mengetahui bagaimana mengukur sebuah satuan yang kita ketahui sebagai energi potensial. Satuan energi secara umum adalah joule dimana sama dengan besarnya work (usaha) yang ditimbulkan dari gaya sebesar 1 newton yang digunakan untuk bergerak sejauh 1 meter (dalam satu arah). Dalam british unit, ini sama halnya dengan kurang dari ¾ pound dari gaya yang dikeluarkan sejauh 1 foot. Masukkan ini dalam suatu persamaan, sama halnya dengan I joule energi yang digunakan untuk mengangkat berat ¾ pound setinggi 1 kaki dari tanah, atau menjatuhkan sesuatu dengan jarak 1 kaki menggunakan parallel pulling dengan ¾ pound. Maka kesimplannya, 1 volt sama dengan 1 joule energi potensial per 1 couloumb. Maka 9 volt baterai akan melepaskan energi sebesar 9 joule dalam setiap couloum dari electron yang bergerak pada sebuah rangkian.
Satuan dan symbol dari satuan elektro ini menjadi sangat penting diketahui ketika kita mengeksplorasi hubungan antara mereka dalam sebuah rangkaian. Yang pertama dan mungkin yang sangat penting hubungan antara tegangan, arus dan hambatan ini disebut hokum ohm. Ditemukan oleh Georg Simon Ohm dan dipublikasikannya pada sebuah paper pada tahun 1827, The Galvanic Circuit Investigated Mathematically. Prinsip ohm ini adalah besarnya arus listrik yang mengalir melalui sebuah penghantar metal pada rangkaian, ohm menemukan sebuah persamaan yang simple, menjelaskan bagaimana hubungan antara tegangan, arus, dan hambatan yang saling berhubungan.
HUKUM OHM
E = I R
I = E / R
R = I / E
Kesimpulan :
• Tegangan dinyatakan dengan nilai volts disimbolkan dengan E atau V.
• Arus dinyatakan dengan amps, dan diberi symbol I
• Hambatan dinyatakan dengan ohms diberi symbol R
• Hukum Ohm: E = IR ; I = E/R ; R = E/I
Besarnya daya pada suatu rangkaian dapat di hitung dengan :
P = V . I atau P = I2 . R atau P = V2/ R
Dimana :
P : daya, dalam satuan watt
V : tegangan dalam satuan volt
I : arus dalam satuan ampere
Contoh Soal Latihan:
Sebuah bangunan rumah tangga memakai lampu dengan tegangan pada instalansi lampu rumah tangga tersebut adalah 220 Volt, dan arus yang mengalir pada lampu tersebut adalah 10 ampere, berapakah hambatan pada lampu tersebut, hitunglah?
JAWAB :
dik :
V = 220 Volt
I = 10 Amper
Dit : hambatan…………….?
JAWAB
R = V/R
R = 220/10 = 22 ohm
Jadi hambatan yang mengalir adalah 22 ohm
Contoh Soal Latihan:
Didalam suatu rumah tinggal, terpasang sebuah lampu dengan tegangan 220 Volt, setelah di ukur dengan amper meter arusnya adalah 2 ampere, hitunglah daya yang di serap lampu tersebut ?
JAWAB :
dik :
V = 220 Volt
I = 2 Amper
Dit : Daya…………….?
JAWAB
P = V.I
P = 220. 2 = 440 Watt
Kamis, 22 Juli 2010
Keseimbangan Benda Tegar
Telah dikatakan sebelumnya bahwa suatu benda tegar dapat mengalami gerak translasi (gerak lurus) dan gerak rotasi. Benda tegar akan melakukan gerak translasi apabila gaya yang diberikan pada benda tepat mengenai suatu titik yang yang disebut titik berat.
Benda akan seimbang jika pas diletakkan di titik beratnya
Benda akan seimbang jika pas diletakkan di titik beratnya
Titik berat merupakan titik dimana benda akan berada dalam keseimbangan rotasi (tidak mengalami rotasi). Pada saat benda tegar mengalami gerak translasi dan rotasi sekaligus, maka pada saat itu titik berat akan bertindak sebagai sumbu rotasi dan lintasan gerak dari titik berat ini menggambarkan lintasan gerak translasinya.
Mari kita tinjau suatu benda tegar, misalnya tongkat pemukul kasti, kemudian kita lempar sambil sedikit berputar. Kalau kita perhatikan secara aeksama, gerakan tongkat pemukul tadi dapat kita gambarkan seperti membentuk suatu lintasan dari gerak translasi yang sedang dijalani dimana pada kasus ini lintasannya berbentuk parabola. Tongkat ini memang berputar pada porosnya, yaitu tepat di titik beratnya. Dan, secara keseluruhan benda bergerak dalam lintasan parabola. Lintasan ini merupakan lintasan dari posisi titik berat benda tersebut.
Demikian halnya seorang peloncat indah yang sedang terjun ke kolam renang. Dia melakukan gerak berputar saat terjun. sebagaimana tongkat pada contoh di atas, peloncat indah itu juga menjalani gerak parabola yang bisa dilihat dari lintasan titik beratnya. Perhatikan gambar berikut ini.
seorang yang meloncat ke air dengan berputar
seorang yang meloncat ke air dengan berputar
Jadi, lintasan gerak translasi dari benda tegar dapat ditinjau sebagai lintasan dari letak titik berat benda tersebut. Dari peristiwa ini tampak bahwa peranan titik berat begitu penting dalam menggambarkan gerak benda tegar.
Cara untuk mengetahui letak titik berat suatu benda tegar akan menjadi mudah untuk benda-benda yang memiliki simetri tertentu, misalnya segitiga, kubus, balok, bujur sangkar, bola dan lain-lain. Yaitu d sama dengan letak sumbu simetrinya. Hal ini jelas terlihat pada contoh diatas bahwa letak titik berat sama dengan sumbu rotasi yang tidak lain adalah sumbu simetrinya.
Orang ini berada dalam keseimbangan
Orang ini berada dalam keseimbangan
Di sisi lain untuk benda-benda yang mempunyai bentuk sembarang letak titik berat dicari dengan perhitungan. Perhitungan didasarkan pada asumsi bahwa kita dapat mengambil beberapa titik dari benda yang ingin dihitung titik beratnya dikalikan dengan berat di masing-masing titik kemudian dijumlahkan dan dibagi dengan jumlah berat pada tiap-tiap titik. dikatakan titik berat juga merupakan pusat massa di dekat permukaan bumi, namun untuk tempat yang ketinggiannya tertentu di atas bumi titik berat dan pusat massa harus dibedakan.
Selasa, 20 Juli 2010
Video Hujan Meteor Lyrids April 2010
Sebagai informasi, di Indonesia banyak warga bingung bagaimana cara melihat terjadinya hujan meteor seperti ini namun para ahli menyatakan cara melihat hujan meteor Lyrids di Indonesia sebenarnya bisa dengan cara mudah yakni dapat dilihat secara langsung melalui kasat mata atau tanpa menggunakan alat bantu apapun dengan catatan bahwa cuaca di sekitar daerah tempat kita melakukan pengamatan harus memiliki cuaca cerah dan tidak tertutup mendung serta wajib terbebas dari berbagai polusi cahaya yang menggangu pengamatan.
Sabtu, 17 Juli 2010
AYUNAN
Getaran adalah gerak bolak-balik atau gerak periodik disekitar titik tertentu secara periodik.
Gerak Periodik adalah suatu getaran atau gerakan yang dilakukan benda secara bolak-balik melalui jalan tertentu yang kembali lagi ke tiap kedudukan dan kecepatan setelah selang waktu tertentu.
Simpangan adalah jarak antara kedudukan benda yang bergetar pada suatu saat sampai kembali pada kedudukan seimbangnya.
Amplitudo adalah simpangan maksimum yang dilakukan pada peristiwa getaran.
Perioda adalah waktu yang diperlukan untuk melakukan satu kali getaran penuh.
Frekuensi adalah banyaknya getaran penuh yang dapat dilakukan dalam waktu satu detik.
2. Ayunan Sederhana
 Ayunan sederhana atau disebut bandul melakukan gerakan bolak balik sepanjang busur AB.
Ayunan sederhana atau disebut bandul melakukan gerakan bolak balik sepanjang busur AB.Waktu yang diperlukan oleh benda untuk bergerak dari titik A ke titik A lagi disebut Satu Perioda.
Sedangkan banyaknya getaran atau gerak bolak-balik yang dapat dilakukan dalam waktu satu detik disebut Frekuensi.
Frekuensi yang dihasilkan bandul disebut Frekuensi Alamiah.
Frekuensi Alamiah adalah frekuensi yang ditimbulkan dari ayunan tanpa adanya pengaruh luar.
Untuk Mengetahui besarnya gaya yang mempengaruhi gerak ayunan dapat digunakan persamaan berikut ini :



Dimana :
F :
m :
g : Percepatan gravitasi (ms-2)
θ : Sudut simpangan (…o)
l : Panjang tali (m)
x : Simpangan getar (m)
Simpangan getar (A) dapat diketahui besarnya melalui persamaan sebagai berikut :
 Dimana :
Dimana : A : Simpangan getar (Amplitudo) (m)
θ : Sudut deviasi (…o)
l : Panjang tali (m)
Sedangkan perioda getaran pada ayunan sederhana dapat diketahui melalui persamaan sebagai berikut :
T : Perioda getaran (S)
phi : 3,14 ( 22/7)
l : Panjang tali (m)
g : Percepatan gravitasi (ms-2)
Frekuensi getaran dapat dicari dengan menggunakan persamaan sebagai berikut :



Dimana :
f : Frekuensi getaran (Hz)
phi : 3,14 (22/7)
g : Percepatan gravitasi (ms-2)
l : Panjang tali (m)
T : Periode getaran (s)
SOAL
Sebuah bandul memiliki massa 100 gr dengan panjang tali 40 cm. Apabila percepatan gravitasi bumi 10 ms-2 dan bandul tersebut diberi sudut simpangan sebesar 10o. Tentukanlah amplitudo getaran dan
3. Pegas
Getaran pada pegas memiliki frekuensi alamiah sendiri. Waktu yang diperlukan oleh benda untuk bergerak dari titik A kembali lagi ke titik A lagi disebut satu perioda dimana besarnya tergantung pada
Besarnya
Dimana :
F :
k : Konstanta
x : Simpangan (m)
Konstanta
 Dimana :
Dimana :k : Konstanta pegas (N/m)
m :
ω : Kecepatan sudut dari gerak pegas
Sedangkan untuk mengetahui besarnya frekuensi getarannya melalui persamaan sebagai berikut :
 Dimana :
Dimana : f : Frekuensi getaran (Hz)
phi: 3,14 (22/7)
k : Konstanta
m :
Dan besarnya perioda getar dapat diketahui melalui persamaan sebagai berikut :
 Dimana :
Dimana : T : Perioda getar
phi : 3,14 (22/7)
m :
k : Konstanta
SOAL
Sebuah pegas dengan tetapan4. Hukum Kekekalan Energi Mekanik Pada Getaran
Besarnya energi mekanik dari suatu benda yang bergerak secara periodik adalah tetap.
Energi mekanik adalah jumlah dari energi kinetik dan energi potensial.
Di dalam setiap getaran energi potensial dan energi kinetik besarnya selalu berubah-ubah tetapi memiliki jumlah yang tetap.
Besarnya energi potensial dari benda yang bergetar secara periodik dapat diketahui melalui persamaan sebagai berikut :
 Dimana :
Dimana :Ep : Energi Potensial
k : Konstanta
y : Simpangan getaran
Jumat, 16 Juli 2010
Peta Konsep Optika Geometri

Kalau kita membahas Optic berarti membahas tentang konsep cahaya. Teori Cahaya ada dua konsep fisika yang dipakai, yaitu Cahaya dianggap sebagai partikel dan Cahaya sebagai Gelombang. Optika adalah ilmu yang membahas tentang konsep cahaya sebagai gelombang. Optika dibagi menjadi Optika Geometri (pemantulan dan Pembiasan) dan Optika Fisis (Difraksi, interferensi atau polarisasi).
Terdapat tiga prinsip dalam Optika Geometri yaitu bentuk lintasan cahaya, Hukum Pemantulan dan Hukum Pmbiasan.
PEMANTULAN CAHAYA
Pada medium Homogen Cahaya merambat lurus. Pemantulan adalah pengembalian dari suatu berkas cahaya ketika bertemu dengan bidang batas antara dua medium. Perhatikanlah video pemantulan cahaya berikut:
Hukum Pemantulan.
Hukum Pemantulan menyatakan sebagai berikut :
- Sinar datang, sinar pantul, dan garsi Normal terletak dalam satu bidang datar.
- Sudut datang (i) sama dengan sudut pantul (r)
ALAT-ALAT OPTIK
Cermin dan lensa serta prinsip kerjanya memberikan sarana pemahaman bagi pemanfaatannya untuk mempermudah dan membantu kehidupan manusia. Alat-alat yang bekerja berdasarkan prinsip optik (cermin dan lensa) digolongkan sebagai alat optik.
Mata
Salah satu alat optik alamiah yang merupakan salah satu anugerah dari Sang Pencipta adalah mata. Di dalam mata terdapat lensa kristalin yang terbuat dari bahan bening, berserat, dan kenyal. Lensa kristalin atau lensa mata berfungsi mengatur pembiasan yang disebabkan oleh cairan di depan lensa. Cairan ini dinamakan aqueous humor. Intensitas cahaya yang masuk ke mata diatur oleh pupil.

Bagian-bagian mata
Cahaya yang masuk ke mata difokuskan oleh lensa mata ke bagian belakang mata yang disebut retina. Bentuk bayangan benda yang jatuh di retina seolah-olah direkam dan disampaikan ke otak melalui saraf optik. Bayangan inilah yang sampai ke otak dan memberikan kesan melihat benda kepada mata. Jadi, mata dapat melihat objek dengan jelas apabila bayangan benda (bayangan nyata) terbentuk tepat di retina.
Lensa mata merupakan lensa yang kenyal dan fleksibel yang dapat menyesuaikan dengan objek yang dilihat. Karena bayangan benda harus selalu difokuskan tepat di retina, lensa mata selalu berubah-ubah untuk menyesuaikan objek yang dilihat. Kemampuan mata untuk menyesuaikan diri terhadap objek yang dilihat dinamakan daya akomodasi mata.

daya akomodasi mata
Saat mata melihat objek yang dekat, lensa mata akan berakomodasi menjadi lebih cembung agar bayangan yang terbentuk jatuh tepat di retina. Sebaliknya, saat melihat objek yang jauh, lensa mata akan menjadi lebih pipih untuk memfokuskan bayangan tepat di retina.
Titik terdekat yang mampu dilihat oleh mata dengan jelas disebut titik dekat mata (punctum proximum/PP). Pada saat melihat benda yang berada di titik dekatnya, mata dikatakan berakomodasi maksimum. Titik dekat mata disebut juga dengan jarak baca normal karena jarak yang lebih dekat dari jarak ini tidak nyaman digunakan untuk membaca dan mata akan terasa lelah. Jarak baca normal atau titik dekat mata adalah sekitar 25 cm.
Adapun, titik terjauh yang dapat dilihat oleh mata dengan jelas disebut titik jauh mata (punctum remotum/PR). Pada saat melihat benda yang berada di titik jauhnya, mata berada dalam kondisi tidak berakomodasi. Jarak titik jauh mata normal adalah di titik tak hingga (~).
Rabun Jauh dan Cara Memperbaikinya
Orang yang menderita rabun jauh atau miopi tidak mampu melihat dengan jelas objek yang jauh tapi tetap mampu melihat dengan jelas objek di titik dekatnya (pada jarak 25 cm). titik jauh mata orang yang menderita rabun jauh berada pada jarak tertentu (mata normal memiliki titik jauh tak berhingga).
Rabun jauh dapat diperbaiki dengan menggunakan lensa divergen yang bersifat menyebarkan (memencarkan) sinar. Lensa divergen atau lensa cekung atau lensa negatif dapat membantu lensa mata agar dapat memfokuskan bayangan tepat di retina.

miopi dikoreksi menggunakan lensa negatif
Jarak fokus lensa dan kuat lensa yang digunakan untuk memperbaiki mata yang mengalami rabun jauh dapat ditentukan berdasarkan persamaan lensa tipis dan rumus kuat lensa.
![]()
![]() Di sini jarak s adalah jarak tak hingga (titik jauh mata normal), dan s’ adalah titik jauh mata (PR). Prinsip dasarnya adalah lensa negatif digunakan untuk memindahkan (memajukan) objek pada jarak tak hingga agar menjadi bayangan di titik jauh mata tersebut sehingga mata dapat melihat objek dengan jelas.
Di sini jarak s adalah jarak tak hingga (titik jauh mata normal), dan s’ adalah titik jauh mata (PR). Prinsip dasarnya adalah lensa negatif digunakan untuk memindahkan (memajukan) objek pada jarak tak hingga agar menjadi bayangan di titik jauh mata tersebut sehingga mata dapat melihat objek dengan jelas.
Rabun Dekat dan Cara Memperbaikinya
Orang yang menderita rabun dekat atau hipermetropi tidak mampu melihat dengan jelas objek yang terletak di titik dekatnya tapi tetap mampu melihat dengan jelas objek yang jauh (tak hingga). Titik dekat mata orang yang menderita rabun dekat lebih jauh dari jarak baca normal (PP > 25 cm).
Cacat mata hipermetropi dapat diperbaiki dengan menggunakan lensa konvergen yang bersifat mengumpulkan sinar. Lensa konvergen atau lensa cembung atau lensa positif dapat membantu lensa mata agar dapat memfokuskan bayangan tepat di retina.

hipermetropi dikoreksi menggunakan lensa positif
Jarak fokus lensa dan kuat lensa yang digunakan untuk memperbaiki mata yang mengalami hipermetropi dapat ditentukan berdasarkan persamaan lensa tipis dan rumus kuat lensa.
![]()
![]() Di sini jarak s adalah jarak titik dekat mata normal (25 cm), dan s’ adalah titik dekat mata (PP). Prinsip dasarnya adalah lensa positif digunakan untuk memindahkan (memundurkan) objek pada jarak baca normal menjadi bayangan di titik dekat mata tersebut sehingga mata dapat melihat objek dengan jelas.
Di sini jarak s adalah jarak titik dekat mata normal (25 cm), dan s’ adalah titik dekat mata (PP). Prinsip dasarnya adalah lensa positif digunakan untuk memindahkan (memundurkan) objek pada jarak baca normal menjadi bayangan di titik dekat mata tersebut sehingga mata dapat melihat objek dengan jelas.
Kaca Pembesar
Kaca pembesar atau lup digunakan untuk melihat benda kecil yang tidak bisa dilihat dengan mata secara langsung. Lup menggunakan sebuah lensa cembung atau lensa positif untuk memperbesar objek menjadi bayangan sehingga dapat dilihat dengan jelas.
 Bayangan yang dibentuk oleh lup bersifat maya, tegak, dan diperbesar. Untuk mendapatkan bayangan semacam ini objek harus berada di depan lensa dan terletak diantara titik pusat O dan titik fokus F lensa. untuk menghasilkan bayangan yang diinginkan, lup dapat digunakan dalam dua macam cara, yaitu dengan mata berakomodasi maksimum dan dengan mata tidak berakomodasi.
Bayangan yang dibentuk oleh lup bersifat maya, tegak, dan diperbesar. Untuk mendapatkan bayangan semacam ini objek harus berada di depan lensa dan terletak diantara titik pusat O dan titik fokus F lensa. untuk menghasilkan bayangan yang diinginkan, lup dapat digunakan dalam dua macam cara, yaitu dengan mata berakomodasi maksimum dan dengan mata tidak berakomodasi.
Lup dapat digunakan dengan mata berakomodasi maksimum untuk mendapatkan perbesaran bayangan yang diinginkan. Agar mata berakomodasi maksimum, bayangan yang terbentuk harus tepat berada di titik dekat mata (s’ = sn = jarak titik dekat mata).
 Perbesaran bayangan yang dihasilkan oleh lup dengan mata berakomodasi maksimum adalah
Perbesaran bayangan yang dihasilkan oleh lup dengan mata berakomodasi maksimum adalah
![]() Dimana P adalah perbesaran lup, sn adalah jarak titik dekat mata (sn = 25 cm untuk mata normal), dan f adalah jarak fokus lup.
Dimana P adalah perbesaran lup, sn adalah jarak titik dekat mata (sn = 25 cm untuk mata normal), dan f adalah jarak fokus lup.
Menggunakan lup dalam keadaan mata berakomodasi maksimum membuat mata menjadi cepat lelah. Agar mata relaks dan tidak cepat lelah, lup digunakan dalam keadaan mata tidak berakomodasi. Untuk mendapatkan perbesaran bayangan yang diinginkan dalam keadaan mata tidak berakomodasi, bayangan yang terbentuk harus berada sangat jauh di depan lensa (jarak tak hingga). dalam hal ini objek harus berada di titik fokus lensa (s = f).
 Perbesaran bayangan yang dihasilkan oleh lup dengan mata tidak berakomodasi adalah
Perbesaran bayangan yang dihasilkan oleh lup dengan mata tidak berakomodasi adalah
![]() Dimana P adalah perbesaran lup, sn adalah jarak titik dekat mata (sn = 25 cm untuk mata normal), dan f adalah jarak fokus lup.
Dimana P adalah perbesaran lup, sn adalah jarak titik dekat mata (sn = 25 cm untuk mata normal), dan f adalah jarak fokus lup.
Mikroskop
Perbesaran bayangan yang dihasilkan dengan menggunakan lup yang hanya menggunakan sebuah lensa cembung kurang maksimal dan terbatas. Untuk mendapatkan perbesaran yang lebih besar diperlukan susunan alat optik yang lebih baik. Perbesaran yang lebih besar dapat diperoleh dengan membuat susunan dua buah lensa cembung. Susunan alat optik ini dinamakan mikroskop yang dapat menghasilkan perbesaran sampai lebih dari 20 kali.
Sebuah mikroskop terdiri atas dua buah lensa cembung (lensa positif). lensa yang dekat dengan objek (benda) dinamakan lensa objektif, sedangkan lensa yang dekat mata dinamakan lensa okuler. Jarak fokus lensa okuler lebih besar daripada jarak fokus lensa objektif.

mikroskop dan bagian-bagiannya

pembentukan bayangan pada mikroskop
Objek yang ingin diamati diletakkan di depan lensa objektif di antara titik Fob dan 2Fob. Bayangan yang terbentuk oleh lensa objektif adalah I1 yang berada di belakang lensa objektif dan di depan lensa okuler. Bayangan ini bersifat nyata, terbalik, dan diperbesar. Bayangan I1 akan menjadi benda bagi lensa okuler dan terletak di depan lensa okuler antara pusat optik O dan titik fokus okuler Fok. Di sini lensa okuler akan berfungsi sebagai lup dan akan terbentuk bayangan akhir I2 di depan lensa okuler. Bayangan akhir I2 yang terbentuk bersifat maya, diperbesar, dan terbalik terhadap objek semula.
Perbesaran yang dihasilkan mikroskop adalah gabungan dari perbesaran lensa objektif dan perbesaran lensa okuler. Perbesaran lensa objektif mikroskop adalah
![]() Dimana Pob adalah perbesaran lensa objektif, s’ob adalah jarak bayangan lensa objektif dan sob adalah jarak objek di depan lensa objektif.
Dimana Pob adalah perbesaran lensa objektif, s’ob adalah jarak bayangan lensa objektif dan sob adalah jarak objek di depan lensa objektif.
Adapun perbesaran lensa okuler mikroskop sama dengan perbesaran lup, yaitu sebagai berikut.
![]()
untuk mata berakomodasi maksimum
![]()
untuk mata tidak berakomodasi
Dimana Pok adalah perbesaran lensa okuler, sn adalah jarak titik dekat mata (untuk mata normal sn = 25 cm), dan fok adalah jarak fokus lensa okuler.
Perbesaran total mikroskop adalah hasil kali perbesaran lensa objektif dan perbesaran lensa okuler. Jadi,
P = Pob × Pok
Hal-hal penting yang perlu diketahui berkaitan dengan mikroskop:
(1) jarak antara lensa objektif dan lensa okuler disebut juga panjang tabung (d). panjang tabung sama dengan penjumlahan jarak bayangan yang dibentuk lensa objektif (s’ob) dengan jarak benda (bayangan pertama) ke lensa okuler (sok).
d = s’ob + sok
(2) menggunakan mikroskop dengan mata berakomodasi maksimum berarti letak bayangan akhir berada di titik dekat mata di depan lensa okuler. Jadi, dapat dituliskan
s’ok = −sn
(3) menggunakan mikroskop dengan mata tidak berakomodasi berarti jarak benda di depan lensa okuler (sok ) berada tepat di titik fokus lensa okuler (fok). Jadi, dapat dituliskan
sok = fok
Teropong Bintang
Bintang-bintang di langit yang letaknya sangat jauh tidak dapat dilihat secara langsung oleh mata. Teropong atau teleskop dapat digunakan untuk melihat bintang atau objek yang letaknya sangat jauh.
Teropong terdiri atas dua lensa cembung, sebagaimana mikroskop. Pada teropong jarak fokus lensa objektif lebih besar daripada jarak fokus lensa okuler (fob > fok). Teropong digunakan dengan mata tidak berakomodasi agar tidak cepat lelah karena teropong digunakan untuk mengamati bintang selama berjam-jam. Dengan mata tidak berakomodasi, bayangan lensa objektif harus terletak di titik fokus lensa okuler. Dengan demikian, panjang teropong (atau jarak antara kedua lensa) adalah
d = fob + fok
dimana fob adalah jarak fokus lensa objektif dan fok adalah jarak fokus lensa okuler.
Adapun perbesaran P yang dihasilkan oleh teropong adalah
![]()
Medan listrik
Dari Wikipedia bahasa Indonesia, ensiklopedia bebas
 Terkini (belum ditinjau)
Terkini (belum ditinjau)Medan listrik adalah efek yang ditimbulkan oleh keberadaan muatan listrik, seperti elektron, ion, atau proton, dalam ruangan yang ada di sekitarnya. Medan listrik memiliki satuan N/C atau dibaca Newton/coulomb. Medan listrik umumnya dipelajari dalam bidang fisika dan bidang-bidang terkait, dan secara tak langsung juga di bidang elektronika yang telah memanfaatkan medan listrik ini dalam kawat konduktor (kabel).
Daftar isi[sembunyikan] |
[sunting] Asal medan listrik
Rumus matematika untuk medan listrik dapat diturunkan melalui Hukum Coulomb, yaitu gaya antara dua titik muatan:
Menurut persamaan ini, gaya pada salah satu titik muatan berbanding lurus dengan besar muatannya. Medan listrik didefinisikan sebagai suatu konstan perbandingan antara muatan dan gaya[1]:
Maka, medan listrik bergantung pada posisi. Suatu medan, merupakan sebuah vektor yang bergantung pada vektor lainnya. Medan listrik dapat dianggap sebagai gradien dari potensial listrik. Jika beberapa muatan yang disebarkan menghasiklan potensial listrik, gradien potensial listrik dapat ditentukan.
[sunting] Konstanta k
Dalam rumus listrik sering ditemui konstanta k sebagai ganti dari  (dalam tulisan ini tetap digunakan yang terakhir), di mana konstanta
(dalam tulisan ini tetap digunakan yang terakhir), di mana konstanta 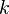 tersebut bernilai [2]:
tersebut bernilai [2]:
yang kerap disebut konstanta kesetaraan gaya listrik [3].
[sunting] Menghitung medan listrik
Untuk menghitung medan listrik di suatu titik  akibat adanya sebuah titik muatan
akibat adanya sebuah titik muatan  yang terletak di
yang terletak di  digunakan rumus [4]
digunakan rumus [4]
[sunting] Penyederhanaan yang kurang tepat
Umumnya untuk melakukan penyederhanaan dipilih pusat koordinat berhimpit dengan titik muatan  yang terletak di
yang terletak di  sehingga diperoleh rumus seperti telah dituliskan pada permulaan artikel ini, atau bila dituliskan kembali dalam notasi vektornya:
sehingga diperoleh rumus seperti telah dituliskan pada permulaan artikel ini, atau bila dituliskan kembali dalam notasi vektornya:
dengan vektor satuan 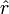

Disarankan untuk menggunakan rumusan yang melibatkan  dan
dan  karena lebih umum, dan dapat diterapkan untuk kasus lebih dari satu muatan dan juga pada distribusi muatan, baik distribusi diskrit maupun kontinu. Penyederhanaan ini juga kadang membuat pemahaman dalam menghitung medan listrik menjadi agak sedikit kabur. Selain itu pula karena penyederhanaan ini hanya merupakan salah satu kasus khusus dalam perhitungan medan listrik (kasus oleh satu titik muatan di mana titik muatan diletakkan di pusat koordinat).
karena lebih umum, dan dapat diterapkan untuk kasus lebih dari satu muatan dan juga pada distribusi muatan, baik distribusi diskrit maupun kontinu. Penyederhanaan ini juga kadang membuat pemahaman dalam menghitung medan listrik menjadi agak sedikit kabur. Selain itu pula karena penyederhanaan ini hanya merupakan salah satu kasus khusus dalam perhitungan medan listrik (kasus oleh satu titik muatan di mana titik muatan diletakkan di pusat koordinat).
[sunting] Tanda muatan listrik
Muatan listrik dapat bernilai negatif, nol (tidak terdapat muatan atau jumlah satuan muatan positif dan negatif sama) dan negatif. Nilai muatan ini akan mempengaruhi perhitungan medan listrik dalam hal tandanya, yaitu positif atau negatif (atau nol). Apabila pada setiap titik di sekitar sebuah (atau beberapa) muatan dihitung medan listriknya dan digambarkan vektor-vektornya, akan terlihat garis-garis yang saling berhubungan, yang disebut sebagai garis-garis medan listrik. Tanda muatan menentukan apakah garis-garis medan listrik yang disebabkannya berasal darinya atau menuju darinya. Telah ditentukan (berdasarkan gaya yang dialami oleh muatan uji positif), bahwa
- muatan positif
(+)akan menyebabkan garis-garis medan listrik berarah dari padanya menuju keluar, - muatan negatif
(-)akan menyebabkan garis-garis medan listrik berarah menuju masuk padanya. - muatan nol
( )tidak menyebabkan adanya garis-garis medan listrik.
[sunting] Gradien potensial listrik
Medan listrik dapat pula dihitung apabila suatu potensial listrik  diketahui, melalui perhitungan gradiennya [5]:
diketahui, melalui perhitungan gradiennya [5]:
dengan
untuk sistem koordinat kartesian.
[sunting] Energi medan listrik
Medan listrik menyimpan energi. Rapat energi suatu medan listrik diberikan oleh [6]
dengan
 adalah permittivitas medium di mana medan listrik terdapat, dalam vakum
adalah permittivitas medium di mana medan listrik terdapat, dalam vakum 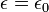 .
. adalah vektor medan listrik.
adalah vektor medan listrik.
Total energi yang tersimpan pada medan listrik dalam suatu volum  adalah
adalah
dengan
 adalah elemen diferensial volum.
adalah elemen diferensial volum.
[sunting] Distribusi muatan listrik
Medan listrik tidak perlu hanya ditimbulkan oleh satu muatan listrik, melainkan dapat pula ditimbulkan oleh lebih dari satu muatan listrik, bahkan oleh distribusi muatan listrik baik yang diskrit maupun kontinu. Contoh-contoh distribusi muatan listrik misalnya:
- kumpulan titik-titik muatan
- kawat panjang lurus berhingga dan tak-berhingga
- lingkaran kawat
- pelat lebar berhingga atau tak-berhingga
- cakram tipis dan cincin
- bentuk-bentuk lain
[sunting] Kumpulan titik-titik muatan
Untuk titik-titik muatan yang tersebar dan berjumlah tidak terlalu banyak, medan listrik pada suatu titik (dan bukan pada salah satu titik muatan) dapat dihitung dengan menjumlahkan vektor medan listrik di titik tersebut akibat oleh masing-masing muatan. Dalam kasus ini lebih baik dituliskan
yang dibaca, medan listrik di titik 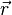 akibat adanya muatan
akibat adanya muatan  yang terletak di
yang terletak di  . Dengan demikian medan listrik di titik
. Dengan demikian medan listrik di titik 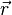 akibat seluruh muatan yang tersebar dituliskan sebagai
akibat seluruh muatan yang tersebar dituliskan sebagai
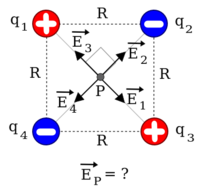
di mana 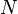 adalah jumlah titik muatan. Sebagai ilustrasi, misalnya ingin ditentukan besarnya medan listrik pada titik
adalah jumlah titik muatan. Sebagai ilustrasi, misalnya ingin ditentukan besarnya medan listrik pada titik 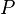 yang merupakan perpotongan kedua diagonal suatu bujursangkar bersisi
yang merupakan perpotongan kedua diagonal suatu bujursangkar bersisi  , di mana terdapat oleh empat buat muatan titik yang terletak pada titik sudut-titik sudut bujursangkar tersebut. Untuk kasus ini misalkan bahwa
, di mana terdapat oleh empat buat muatan titik yang terletak pada titik sudut-titik sudut bujursangkar tersebut. Untuk kasus ini misalkan bahwa  dan
dan  dan ambil pusat koordinat di titik
dan ambil pusat koordinat di titik  untuk memudahkan. Untuk kasus dua dimensi seperti ini, bisa dituliskan pula
untuk memudahkan. Untuk kasus dua dimensi seperti ini, bisa dituliskan pula
yang akan memberikan
sehingga
yang menghasilkan bahwa medan listrik pada titik tersebut adalah nol.
[sunting] Kawat panjang lurus
Kawat panjang lurus merupakan salah satu bentuk distribusi muatan yang menarik karena bila panjangnya diambil tak-hingga, perhitungan muatan di suatu jarak dari kawat dan terletak di tengah-tengah panjangnya, menjadi amat mudah.
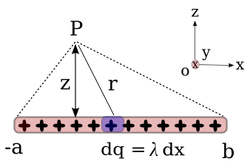
Untuk suatu kawat yang merentang lurus pada sumbu  , pada jarak
, pada jarak  di atasnya, dengan kawat merentang dari
di atasnya, dengan kawat merentang dari 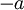 sampai
sampai 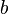 dari titik proyeksi
dari titik proyeksi 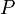 pada kawat, medan listrik di titik tersebut dapat dihitung besarnya, yaitu:
pada kawat, medan listrik di titik tersebut dapat dihitung besarnya, yaitu:
Seperti telah disebutkan di atas, apabila 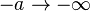 dan
dan  maka dengan menggunakan dalil L'Hospital diperoleh
maka dengan menggunakan dalil L'Hospital diperoleh
Atau bila kawat diletakkan sejajar dengan sumbu-z dan bidang x-y ditembus kawat secara tegak lurus, maka medan listrik di suatu titik berjarak  dari kawat, dapat dituliskan medan listriknya adalah
dari kawat, dapat dituliskan medan listriknya adalah
dengan  adalah vektor satuan radial dalam koordinat silinder:
adalah vektor satuan radial dalam koordinat silinder:
di mana 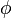 adalah sudut yang dibentuk dengan sumbu-x positif.
adalah sudut yang dibentuk dengan sumbu-x positif.









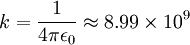

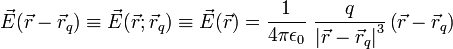
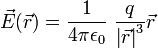













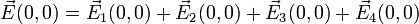

![E_z = \frac{1}{4\pi\epsilon_0}\ \frac{\lambda}{z} \ \left[ \frac{b}{\sqrt{z^2+b^2}} +\frac{a}{\sqrt{z^2+a^2}} \right]](http://upload.wikimedia.org/math/e/5/c/e5c6456573df6a6c19ba66c547ba13ad.png)